A Theory of Quark vs. Gluon Discrimination
Abstract
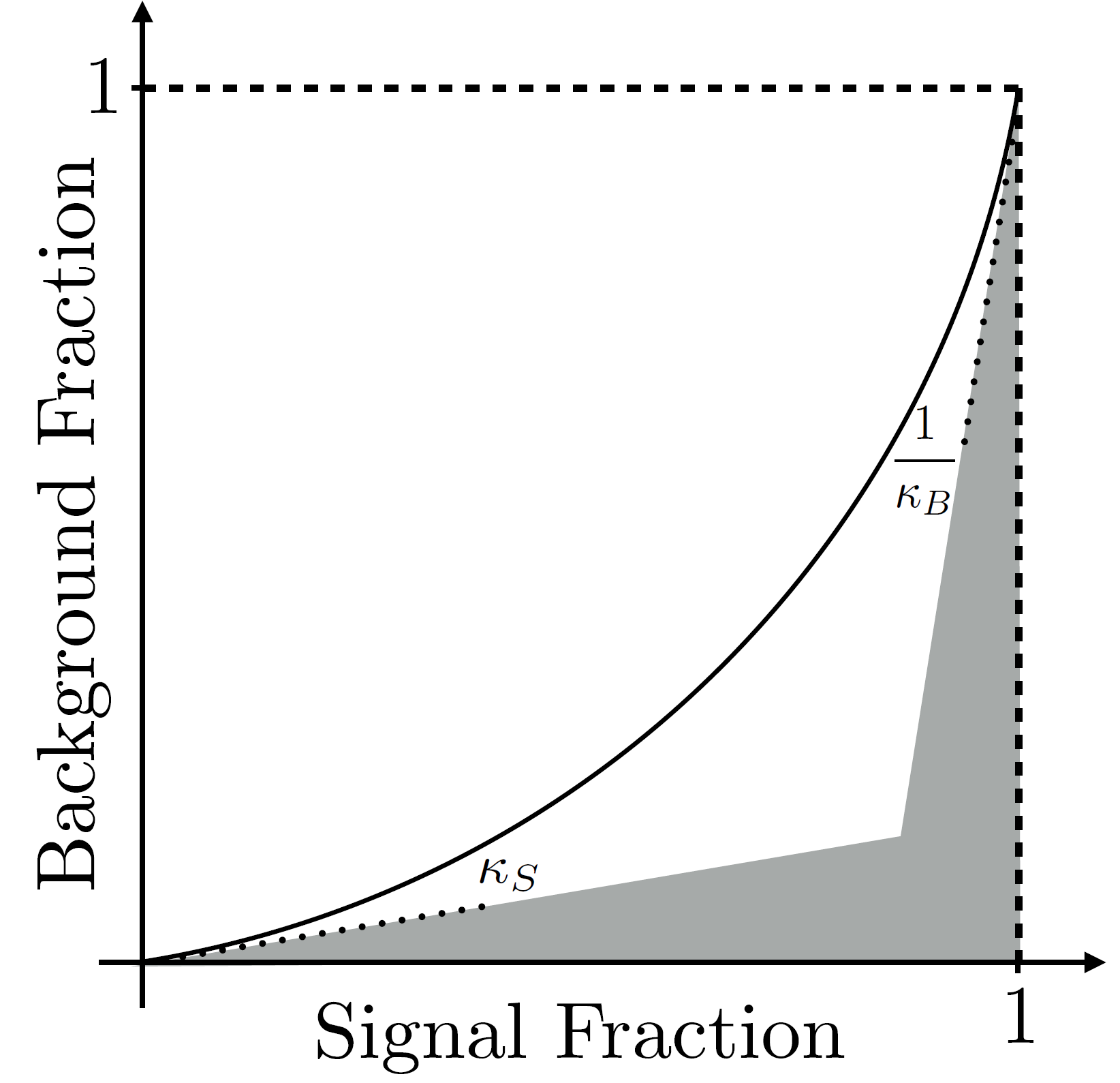
Understanding jets initiated by quarks and gluons is of fundamental importance in collider physics. Efficient and robust techniques for quark versus gluon jet discrimination have consequences for new physics searches, precision strong coupling constant studies, parton distribution function extractions, and many other applications. Numerous machine learning analyses have attacked the problem, demonstrating that good performance can be obtained but generally not providing an understanding for what properties of the jets are responsible for that separation power. In this paper, we provide an extensive and detailed analysis of quark versus gluon discrimination from first-principles theoretical calculations. Working in the strongly-ordered soft and collinear limits, we calculate probability distributions for fixed N-body kinematics within jets with up through three resolved emissions. This enables explicit calculation of quantities central to machine learning such as the likelihood ratio, the area under the receiver operating characteristic curve, and reducibility factors within a well-defined approximation scheme. Further, we relate the existence of a consistent power counting procedure for discrimination to ideas for operational flavor definitions, and we use this relationship to construct a power counting for quark versus gluon discrimination as an expansion in the exponential of the fundamental and adjoint Casimirs. Our calculations provide insight into the discrimination performance of particle multiplicity and show how observables sensitive to all emissions in a jet are optimal. We compare our predictions to the performance of individual observables and neural networks with parton shower event generators, validating that our predictions describe the features identified by machine learning.